机器学习系列(I):决策树算法

一 03 三月 2014

写在前面

好吧，今天我的博客在线下默默地开张了，花了好长时间才把中文显示的问题解决。言归正传，之所以开通这个博客，原因有二：

对已经学过的知识进行梳理，保证学习过程的稳步前进；
敦促自己每周有一定的学习目标,以更好地推进自己的学习.

关于这个博客其他的我就不说了，如果你觉得这个博客有点用，你愿意花点时间看看，我会灰常感激滴。如果你觉得这个博客没什么用，直接忽略就好。此外，这篇博客所有内容均host在Github上，本着分享，协作的精神，如果你愿意而且有时间欢迎投稿至qingyuanxingsi@163.com,I would be much glad to receive your mails.

简介

二三闲话

这是本博客的第一篇博文，也是第一篇关于机器学习方面的博文，因此我想扯些闲话。就我而言，我觉得所有的机器学习算法并不只是模型本身那么简单，背后其实还有一些别的东西，从某种角度来说，它们也是模型的创立者认识世界的方式。

举贝叶斯为例，从他的模型中可能能推断出他也许认为万物皆有联系，所有的事物都不是孤立的，都是相互联系，相互影响的。一个事物的改变会引起其他事物的相应变化，世界是一个相互联系的整体。另，我经常听到人们抱怨这个世界不公平，这个世界并不是他们想要的那种模样；或者说自从多年前姚晨和凌潇肃离婚之后，好多人都不再相信爱情了(just a joke）。虽然说这是生活中再平常不过的桥段，从这两个例子中，也许我们能看到另外一些东西，我们很久很久以前都对这个世界有一些先入为主的认识(prior),我们愿意相信这个世界是公平的，爱情是非常美好的一件事。后来，慢慢的我们发现这个世界其实有很多不公平的事，我们发现这个世界里的爱情没我们想象的那么美好，我们看到了一些真实世界实实在在存在的事情(data),于是我们对于这个世界的认识发生了改变，我们开始相信一些原来不相信的事情，对我们之前深信不疑的事情也不再那么确信。(posterior)(关于这个模型我们下一次说吧).

曾经相信过爱情，后来知道，原来爱情必须转化为亲情才可能持久，但是转化为亲情的爱情，犹如化入杯水中的冰块──它还是冰块吗？
曾经相信过海枯石烂作为永恒不灭的表征，后来知道，原来海其实很容易枯，石，原来很容易烂。雨水，很可能不再来，沧海，不会再成桑田。原来，自己脚下所踩的地球，很容易被毁灭。海枯石烂的永恒，原来不存在。
...
相信与不相信之间，彷佛还有令人沉吟的深度。(龙应台《相信，不相信》）

举上面例子的目的意在说明其实机器学习算法也许并非就是些模型，就是些数学而已，它也许能给我们提供看待世界的另一种角度，也许能带给我们一些有益的思考。关于闲话就说到这儿，以后我们有时间慢慢扯。

Introduction to Decision Trees

所谓决策树，顾名思义，是一种树，一种依托于策略抉择而建立起来的树。决策树中非叶节点(非根节点)均是决策节点，决策节点的取值决定了决策树具体下一步跳到那个节点，每个决策节点的分支则分别代表了决策属性可能的取值；每一个叶节点代表了一个分类属性，即决策过程的完成。从根节点到叶节点的每一条路径代表了一个可能的决策过程。

举个例子，也许大家能对决策树到底是什么有一个更为清楚直观的认识:

一个非常经典的例子是一个女生找对象的过程，在女孩决定是否相亲的过程中可能产生如下对话:

女儿：多大年纪了？
母亲：26。
女儿：长的帅不帅？
母亲：挺帅的。
女儿：收入高不？
母亲：不算很高，中等情况。
女儿：是公务员不？
母亲：是，在税务局上班呢。
女儿：那好，我去见见。

这个女孩的决策过程就是典型的分类树决策。相当于通过年龄、长相、收入和是否公务员对将男人分为两个类别：见和不见。假设这个女孩对男人的要求是：30岁以下、长相中等以上并且是高收入者或中等以上收入的公务员，那么这个可以用下图表示女孩的决策逻辑：

girl

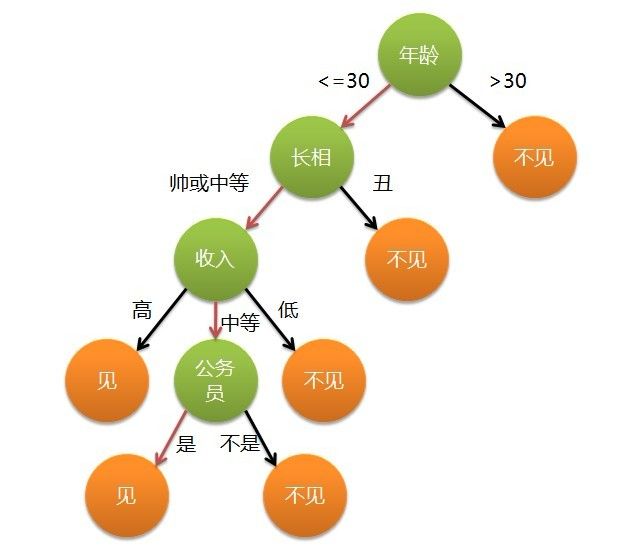
根据奥卡姆剃刀原则(Simpler is better),我们尽可能想构造得到的决策书尽可能的小。因此，如何选择上图中决策属性是所有决策树算法的核心所在。我们尽量在每一步要有限选取最有分辨能力的属性作为决策属性，以保证树尽可能的小。针对决策树，我们主要介绍两种比较典型的算法ID3以及C4.5,另外CART(Classification and Regression Tree)是另外使用的比较多的算法，商用的版本则有C5.0,它主要针对C4.5算法做了很多性能上的优化。具体针对CART以及C5.0的介绍本文将不再涉及。

ID3

ID3算法基本框架

ID3算法是一个由Ross Quinlan发明的用于决策树的算法。它是一个启发式算法，具体算法框架可参见《机器学习》一书中的描述，如下所示: ID3

分裂属性的选取

如上图算法框架所示，判断测试某个属性为最佳的分类属性是ID3的核心问题，以下介绍两个比较重要的概念：信息熵和信息增益。

信息熵

为了精确地定义信息增益，我们先定义信息论中广泛使用的一个度量标准，称为熵(entropy),它刻画了任意样例集的纯度，另一种理解则是用来编码信息所需的最少比特位数。 \begin{equation} Entropy(S) = -\sum_{i=1}^{c} p_ilog(p_i) \end{equation}
其中，$p_i$是属性S属于类别i的概率。

信息增益

已经有了熵作为衡量训练样例集合纯度的标准，现在可以定义属性分类训练数据的效力的度量标准。这个标准被称为“信息增益（information gain）”。简单的说，一个属性的信息增益就是由于使用这个属性分割样例而导致的期望熵降低(或者说，样本按照某属性划分时造成熵减少的期望,个人结合前面理解，总结为用来衡量给定的属性区分训练样例的能力)。更精确地讲，一个属性A相对样例集合S的信息增益$Gain(S,A)$被定义为： \begin{equation} Gain(S,A)=Entropy(S) - \sum_{v \in S_v} \frac{|S_v|}{|S|}Entropy(S_v) \end{equation}
其中： $V(A)$是属性A的值域； $S$是样本集合； $S_v$是S在属性A上取值等于v的样本集合。

对于上述算法框架中迭代的每一步，针对样本集合S,我们分别算出针对每个可能的属性的信息增益值，并选择值最大的那个对应的属性作为我们该步的分裂属性即可。依次迭代，便能构造我们想要的决策树。

Python代码实现

实践出真知，磨刀霍霍，我们小小地实现一下。对于以上提到的ID3算法，基于Python我们给出了相应的源码实现，如下:(本博客中所有源码仅是算法思想的一个比较粗略的实现，很多方面还不成熟，特此说明，以后不再提及)

import numpy as np
import math
import operator

class DTree_ID3:
    def runDT(self, dataset, features):
        classList = [sample[-1] for sample in dataset]
        if classList.count(classList[0]) == len(classList):
            return classList[0]
        if len(dataset[0]) == 1:
            return self.classify(classList)

        max_index = self.Max_InfoGain(dataset) ##index
        max_fea = features[max_index]
        myTree = {max_fea:{}}
        fea_val = [sample[max_index] for sample in dataset]
        unique = set(fea_val);    
        del (features[max_index]) 
        for values in unique:          
            sub_dataset = self.splitDataSet(dataset, max_index, values)         
            myTree[max_fea][values] = self.runDT(sub_dataset,features) 
        features.insert(max_index,max_fea)  
        return myTree

    def classify(self,classList):
        classCount = {}
        for vote in classList:
            if vote not in classCount.keys():
                classCount[vote] = 0
            classCount[vote] += 1
        sortedClassCount = sorted(classCount.iteritems(), key = operator.itemgetter(1), revese = True)
        return sortedClassCount[0][0]

    def Max_InfoGain(self, data_set):
        #compute all features InfoGain, return the maximal one
        Num_Fea = len(data_set[1,:])
        #Num_Tup = len(data_set)
        max_IG = 1
        max_Fea = -1
        for i in range(Num_Fea-1):
            InfoGain = self.Info(data_set[:,[i,-1]])
            if (max_IG > InfoGain):
                max_IG = InfoGain
                max_Fea = i
        return max_Fea

    def Info(self, data):
        dic = {}
        for tup in data:
            if tup[0] not in dic.keys():
                dic[tup[0]] = {}
                dic[tup[0]][tup[1]] = 1
            elif tup[1] not in dic[tup[0]]:
                dic[tup[0]][tup[1]] = 1
            else:
                dic[tup[0]][tup[1]] += 1

        S_total = 0.0
        for key in dic:
            s = 0.0
            for label in dic[key]:
                s += dic[key][label]
            S_each = 0.0
            for label in dic[key]:
                prob = float(dic[key][label]/s)
                if prob !=0 :
                    S_each -= prob*math.log(prob,2)
            S_total += s/len(data[:,0])*S_each
        return S_total

    def splitDataSet(self,dataSet,featureIndex,value):
        subDataSet = []
        dataSet = dataSet.tolist()
        for sample in dataSet:
            if sample[featureIndex] == value:
                reducedSample = sample[:featureIndex]  
                reducedSample.extend(sample[featureIndex+1:])  
                subDataSet.append(reducedSample)
        return np.asarray(subDataSet)

if __name__ == "__main__":
    dataSet = np.array([["Cool","High","Yes","Yes"],["Ugly","High","No","No"],
               ["Cool","Low","No","No"],["Cool","Low","Yes","Yes"],
               ["Cool","Medium","No","Yes"],["Ugly","Medium","Yes","No"]])
    featureSet = ["Appearance","Salary","Office Guy"]
    dTree = DTree_ID3()
    tree = dTree.runDT(dataSet,featureSet)
    print(tree)

C4.5

C4.5决策树在ID3决策树的基础之上稍作改进，并克服了其两大缺点:

用信息增益选择属性偏向于选择分枝比较多的属性，即取值多的属性;
不能处理连续属性.

对于这两个问题，C4.5都给出了具体的解决方案，以下做一个简要的阐述。

信息增益率

C4.5选取了信息增益率作为选择决策属性的依据，克服了用信息增益来选择属性时偏向选择值多的属性的不足。信息增益率定义为： \begin{equation} GainRatio(S,A)=\frac{Gain(S,A)}{SplitInfo(S,A)} \end{equation} 其中$Gain(S,A)$和ID3算法中的信息增益计算相同，而$SplitInfo(S,A)$代表了按照属性A分裂样本集合S的广度和均匀性。 \begin{equation} SplitInfo(S,A)=-\sum_{i=1}^{c} \frac{|S_i|}{|S|}log\frac{|S_i|}{|S|} \end{equation} 其中$S_i$表示根据属性A分割S而成的样本子集;

处理连续属性

对于离散值，C4.5和ID3的处理方法相同，对于某个属性的值连续时，假设这这个节点上的数据集合样本为total，C4.5算法进行如下处理：

将样本数据该属性A上的具体数值按照升序排列，得到属性序列值：${A_1,A_2,A_3,...,A{total}}$
在上一步生成的序列值中生成total-1个分割点。第i个分割点的取值为$A_i$和$A_{i+1}$的均值，每个分割点都将属性序列划分为两个子集;
计算每个分割点的信息增益(Information Gain),得到total-1个信息增益。}
对分裂点的信息增益进行修正：减去log2(N-1)/|D|，其中N为可能的分裂点个数，D为数据集合大小。
选择修正后的信息增益值最大的分类点作为该属性的最佳分类点
计算最佳分裂点的信息增益率(Gain Ratio)作为该属性的Gain Ratio
选择Gain Ratio最大的属性作为分类属性。

总结

决策树方法是机器学习算法中比较重要且较易于理解的一种分类算法，本文介绍了两种决策树算法，ID3和C4.5.决策树算法的核心在于分裂属性的选取上，对此，ID3采用了信息增益作为评估指标，但是ID3也有不能处理连续属性值和易于选取取值较多的属性，C4.5对这两个问题都给出了相应的解决方案。